[R] 기초통계량

6. 기초통계량

 

6.1 데이터 분석 과정

6.1.1 정의 단계: 문제의 정의

고객으로부터 최대한의 정보를 얻어내야 함

 

6.1.2 분해 단계: 작은 단위로 분할한 후에 단계별로 해결

확보한 데이터를 분할된 단위에 맞추어 수집하거나 재구성

고객이 제공한 문제의 본질을 이해하고 분석 가능한 작은 단위로 문제를 분할한 후에 분석 수행

문제의 분해는 결과에 대한 예측을 기반으로 실행함

 

6.1.3 평가 단계

주어진 문제와 고객이 알고자 하는 것을 기준으로 현재의 시점에서 결과를 평가하는 단계

 

6.1.4 결정 단계

평가가 완료된 후 분석가의 결정을 전달하는 과정

데이터 분석 모델을 확정하고 데이터를 분석하여 최종적인 분석가의 의견을 확정하는 단계

 

6.1.5 반복 단계

새로운 자료나 상황이 발생할 경우 이미 실행한 단계를 다시 수행해야 함

 

 

6.2 데이터의 유형

6.2.1 범주형 데이터(Categorical Data)

사전에 정해진 특정 유형으로 분류되는 데이터

ex) 방의 크기: 대, 중, 소

 

6.2.1.1 명목형: 값들 간의 크기 비교가 불가능

ex) 정치적 성향(좌파, 우파), 성별 등

 

6.2.1.2 순서형: 대, 중, 소와 같이 값에 순서를 매길 수 있는 경우

ex) 성적 데이터, 방의 크기

 

6.2.2 연속형 데이터(Continuous Data): 정량적 데이터

6.2.2.1 등간척도: 섭씨온도, 화씨온도, 시간 등

6.2.2.2 비율척도: 키, 몸무게, 점수, 관찰빈도 등

변수 유형	자료 유형	예
질적변수	명목형 변수	성별, 혈액형
	순서형 변수	학력, 설문문항
양적변수	이산형 변수	가족수, 수강과목 수
	연속형 변수	키, 몸무게

 

 

6.3 데이터 시각화 방법

6.3.1 기초통계량(평균, 분산 등)

전체 데이터의 특성을 표현하는 수치

 

6.3.2 산포도(산점도): 전체 데이터가 어떤 특징을 가지는지 보여줌

• x축 독립변수(영향을 미치는 변수, 원인)
• y축 종속변수(결과)

 

6.3.3 히스토그램

데이터를 구간별로 나누어 도수를 표시함으로써 특징을 보여줌

 

 

6.4 기초통계량

6.4.1 최대값, 최소값

 

6.4.2 최빈값

가장 많이 관찰된 값

 

6.4.3 평균값

 

6.4.4 중앙값

 

6.4.5 표준편차

 

6.4.6 사분위수

	R 함수	설명
자료의 갯수	length()
최소값	min()
최대값	max()
범위	range()
최빈값		자료 중 빈도수가 가장 많은 값
평균	mean()
중앙값	median()	자료를 순서대로 나열했을 경우 중앙에 있는 값
표준편차	sd()	평균을 중심으로 자료가 퍼진 정도
제1사분위수	qunatile()	자료를 순서대로 나열했을 때 25% 위치의 값
제3사분위수		자료를 순서대로 나열했을 때 75% 위치의 값
사분위수 범위	IQR()	제3사분위수-제1사분위수

 

 

6.5 실습 예제

1. 데이터를 R로 읽어들인다.
2. 읽어들인 데이터로 그래프를 그린다.
3. 읽어들인 데이터의 기초통계량을 구한다.

 

데이터의 빈도수 확인

히스토그램

 

 

boxplot

상자수염그림 - 두 그룹의 분포를 비교할 목적

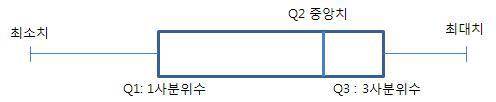
• 사분위수: 자료를 순서대로 정렬한 후 4등분한 것
  0%(Lowest), 25%(Q1), 50%(Q2), 75%(Q3), 100%(Highest)
• Q3-Q1: 사분위수 범위(Interquartile Range, IQR) 상자의 길이

 

 

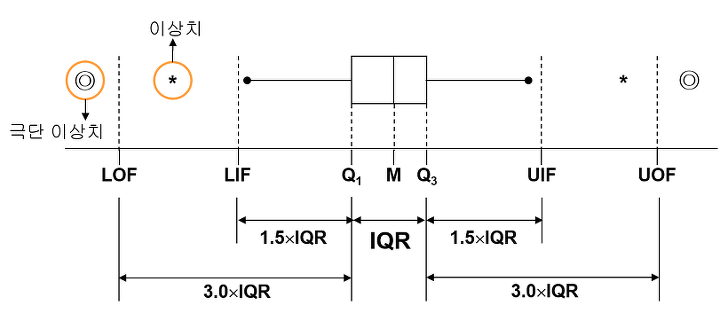
• LIF(Lower Inner Fence): 하 내부울타리 Q1 - 1.5 x IQR
• UIF(Upper Inner Fence): 상 내부울타리 Q3 + 1.5 x IQR
• LOF(Lower Outer Fence): 하 외부울타리 Q1 - 3.0 x IQR
• UOF(Upper Outer Fence): 상 외부울타리 Q3 + 3.0 x IQR

boxplot(flour, diet, names = c("flour", "diet"))

 

기초 통계량 계산

# 합계
sum(total)

# 사분위수
quantile(total)
#    0%   25%   50%  75% 100%
# -8.00 -3.25 -2.00 0.25 3.00

# min, 1Q, median, 3Q, max
# -8.0, -3.5, -2.0, 0.5, 3.0
fivenum(total)
summary(total)

# 상관계수
cor(flour, diet)

 

6.6 커피 판매량 데이터셋

# install.packages("ggplot2")
library(ggplot2)

cafe <- read.csv("D:/data/cafe/data.csv", header = T)

# print(head(cafe))
print(cafe$Coffees)
print(sort(cafe$Coffees))  # 자료 정렬

 

6.6.1 최댓값과 최솟값

# 정렬된 값 중 첫 번째 값
sort(cafe$Coffees)[1]

# 내림차순 정렬
sort(cafe$Coffees, decreasing = TRUE)

# 내림차순 정렬된 값 중 첫 번째 값
sort(cafe$Coffees, decreasing = TRUE)[1]

# 최솟값
min(cafe$Coffees)

# 최댓값
max(cafe$Coffees)

# 하루 주문량은 3~48잔임을 알 수 있음

 

6.6.2 최빈값(mode)

가장 많이 관찰된 값, 가장 빈도가 높은 값

# seq(0, 50, by = 10): 0~50까지 10씩 증가
# right = F: 마지막 값은 선택하지 않음
table(cut(cafe$Coffees, breaks = seq(0, 50, by = 10), right = F))

# 0~9잔: 9, 10~19잔: 8, 20~29잔: 17

 

ca <- cafe$Coffees
stem(ca)

# 십의 자리가 줄기, 일의 자리가 잎
# 줄기-잎 그림: 자료를 순서대로 나열한 후 적당한 단위로 나눠 줄기 부분을 만들고 각 값을 줄기 부분에 붙인 그림

 

6.6.3 평균값

ca <- cafe$Coffees

# 평균값 계산
mean(ca)

 

# ca 변수에 결측값을 덧붙임
ca <- c(ca, NA)
tail(ca, n = 5)

 

# 결측값이 있으므로 평균값이 계산되지 않음
mean(ca)

# 결측값을 제외하고 평균 계산
mean(ca, na.rm = T)

 

6.6.4 중앙값, 중위수(median)

자료 전체의 중심 위치값

rc <- cafe$Coffees
rc

# 오름차순 정렬
sort(rc)

# 중앙값
median(rc)

 

height <- c(164, 166, 168, 170, 172, 174, 176)

# 평균값
mean(height)

 

# 중앙값
median(height)

 

6.6.5 분산, 표준편차

# 편차(deviation): 개별 관찰 값과 평균과의 차이
# 편차 값을 모두 더하면 0이 되므로 의미가 없고 제곱을 해야 한다.
height.dev <- height - mean(height)
height.dev

 

# 분산(Variance, 편차 제곱의 평균)
var(height)

 

# 표준편차
sd(height)

 

ca <- cafe$Coffees
ca.m <- mean(ca)
ca.sd <- sd(ca)

# cat() 함수: 문자열 연결 함수
cat("평균 판매량: ", round(ca.m, 1), ", 표준편차: ", round(ca.sd, 2))

 

coffee <- cafe$Coffees
juice <- cafe$Juices

# 커피 판매량 평균값
(coffee.m <- mean(coffee))

 

# 커피 판매량의 표준편차
(coffee.sd <- sd(coffee))

11.080480958847

 

# 주스 판매량 평균값
(juice.m <- mean(juice))

4.93617021276596

 

# 주스 판매량의 표준편차
(juice.sd <- sd(juice))

3.70313765503484

 

# 커피 판매량의 변동계수
(coffee.cv <- round(coffee.sd / coffee.m, 3)

0.515

 

# 주스 판매량의 변동계수
(juice.cv <- round(juice.sd / juice.m, 3))

# 표준편차 값을 보면 커피가 훨씬 크지만, 변동계수를 볼 때 주스가 더 크다.
# 즉, 주스 판매량의 변동 폭이 더 크다는 것을 알 수 있다.

0.75

 

6.6.6 사분위수 범위와 상자 도표

(qs <- quantile(coffee))
# 25%가 되는 값(제1사분위수, Q1) 12
# 50%가 되는 값(제2사분위수, Q2) 23
# 75%가 되는 값(제3사분위수, Q3) 30
# 100%가 되는 값(제4사분위수, Q4)

# 사분위수 범위(InterQuartile Range, Q3 - Q1)
IQR(coffee)

bp <- boxplot(coffee, main = "커피 판매량에 대한 상자 도표")

# 상자의 아랫변 Q1, 상자 중앙의 굵은 선 Q2, 상자의 윗변 Q3

 

hist(coffee)

 

# 제동거리의 히스토그램
hist(cars$dist, breaks = seq(0, 120, 10))

 

# 상자 도표와 이상치
boxplot(cars$dist)

# 상자 도표에서 이상치는 작은 원으로 표시됨